国际知名学术期刊封面文章报道深圳超算研究成果

近日，深圳超算中心副研究员徐奇门博士参与的科研团队在《ChemPhysChem》期刊上发表了一篇题为 Self-Consistent Convolutional Density Functional Approximations: Application to Adsorption at Metal Surfaces（《自洽卷积密度泛函近似：金属表面吸附的应用》）的科研论文（论文链接：https://doi.org/10.1002/cphc.202300688）。这项研究由佐治亚理工学院、国家超级计算深圳中心、丰田研究所及布朗大学的多位研究人员共同完成，展示了在密度泛函理论（DFT）中引入全新卷积方法的巨大潜力。徐奇门博士为该论文的第二作者。该文章因其创新性和重要性受到了期刊编委会和评审专家的高度评价，并被遴选为当期封面文章（ChemPhysChem 10/2024, 期刊封面链接：https://doi.org/10.1002/cphc.202400462）。

图1 ChemPhysChem Volume 25, Issue 10. (2024) 期刊封面

密度泛函理论（DFT）是计算化学、材料科学和固态物理学中广泛使用的工具，旨在通过近似薛定谔方程来预测化学系统的电子结构和性质。尽管DFT在处理大规模和半周期系统时具有较高的速度和准确性，但现有的交换-关联（Exchange-Correlation, XC）泛函在多电子相互作用的近似上仍存在显著局限。现有的多种XC泛函几乎都基于“雅各布阶梯”（Jacob’s Ladder）的输入层次结构。

在本项研究中，研究人员提出了一种突破传统“雅各布阶梯”方法的新途径，利用任意卷积核与电子密度的卷积来构建XC泛函。这种方法通过引入卷积核的变分导数，与广义梯度近似（GGA）保持一致，并提供了基于卷积核的多极特征的变分导数方程。研究团队推导了这些泛函的变分导数，并展示了其与广义梯度近似（GGA）的相容性，并提供了基于卷积核多极特征的变分导数方程。团队开发了一种名为PBEq的概念验证泛函，该泛函基于PBEα框架，并将PBEα框架中的常数α推广成电子密度单极子的空间分辨函数。该泛函允许在不同空间点使用不同的GGA泛函，同时遵循PBE约束。

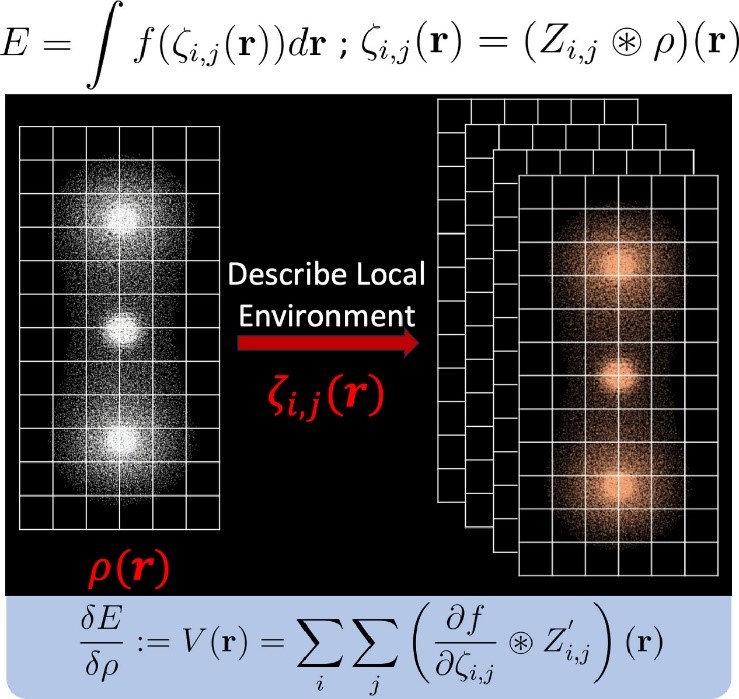
图2 自洽卷积密度泛函近似示意图

研究团队将该方法部署至实空间DFT计算软件SPARC中（徐奇门博士为该软件的第一作者），通过对小分子、金属和表面催化剂的测试，结果表明，这种方法在同时优化多种性质方面具有巨大潜力。研究团队特别指出，误差抵消和XC势在数据驱动的泛函设计中具有重要意义。在具体应用上，研究团队对CO在Pt、Cu和Rh的(111)表面上的吸附能进行了测试。结果显示，PBEq泛函能够正确区分CO在Pt(111)表面上的吸附位点，其准确性至少与现有的RPBE和其他GGA泛函相当。这项研究不仅为化学、材料和表面科学中的XC泛函设计提供了新的思路，也展示了数据驱动的方法在XC泛函设计中的巨大潜力。通过对电子密度进行三维卷积处理，研究团队为未来的密度泛函设计开辟了全新的道路。这种新方法的提出和验证，为未来更多系统的准确模拟和预测提供了可能。随着研究的深入，我们期待这些创新方法能够在更多实际应用中发挥作用，推动科学研究的不断进步。